
The Complex-Time Frame
The following article is extracted from Chapter III of the Duality of Time book, and some of the details are discussed further in other chapters, as well as Volume III that is the Ultimate Symmetry.
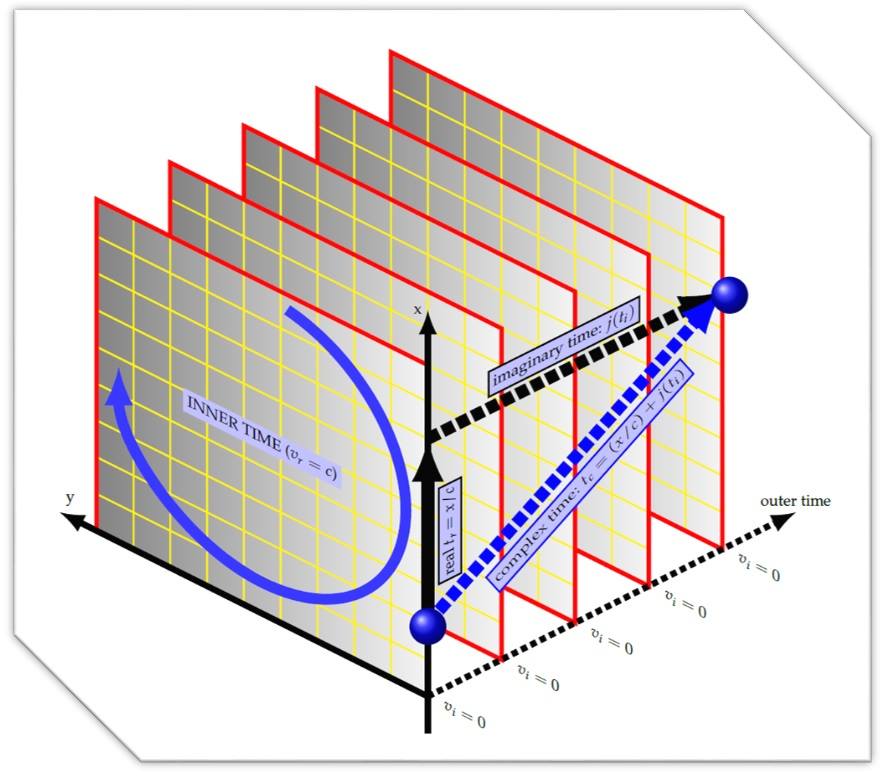
The Duality of Time implies that normal time is actually imaginary or latent with relation to the real flow of time that is creating space and matter. Therefore, the non-Euclidean Minkowski space-time coordinates 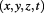 will be a special approximation of the Euclidean space coordinates
will be a special approximation of the Euclidean space coordinates 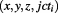 , or time coordinates:
, or time coordinates: 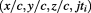 where
where 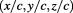 or
or 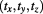 represent the inner real part of time:
represent the inner real part of time: 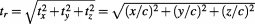 , and
, and 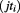 represents the outer imaginary time, so the total complex time is
represents the outer imaginary time, so the total complex time is 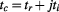 , where
, where 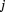 is the split-imaginary unit which defines hyperbolic numbers, thus:
is the split-imaginary unit which defines hyperbolic numbers, thus: 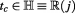 , and its modulus is
, and its modulus is 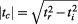 . These hyperbolic numbers have been also called: tessarines, motors, bireal, perplex, semi-complex, or split-complex, but in this book, unless otherwise stated, imaginary and complex refer to these hyperbolic numbers
. These hyperbolic numbers have been also called: tessarines, motors, bireal, perplex, semi-complex, or split-complex, but in this book, unless otherwise stated, imaginary and complex refer to these hyperbolic numbers 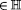 .
.
Hyperbolic geometry was used in the early formulation of Special Relativity to represent Lorentz boost as a rotation in the imaginary plane, but it will be shown in section 2 below that under the new Euclidean complex-time frame, Lorentz transformations will be valid between inertial and non-inertial frames alike, because the dynamic relation between the real and imaginary parts of time implies that the instantaneous velocity in the imaginary time is always zero (see Figure 5.1), whether the object is accelerating or not. Therefore, in addition to Lorentz boost, this essential characteristic of the dynamic and granular complex-time structure, allows direct derivation of the equivalence principle that lead to General Relativity. This will be discussed further in sections 3, 3.2 and 3.5 below.
The actual flow of time, including the inner and outer levels, can be represented in terms of complex Euclidean space as absolute reference frame: 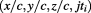 or
or 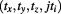 , or simply:
, or simply: 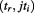 . In this abstract complex frame, space and time are absolute, as they were originally treated in the classical Newtonian mechanics, but now empty space is
void, because it does not have any physical reality, to differentiate it from vacuum that is the dynamic aether or quintessence. So, for void both the real and imaginary parts are null:
. In this abstract complex frame, space and time are absolute, as they were originally treated in the classical Newtonian mechanics, but now empty space is
void, because it does not have any physical reality, to differentiate it from vacuum that is the dynamic aether or quintessence. So, for void both the real and imaginary parts are null: 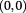 , while for vacuum only the imaginary part is null:
, while for vacuum only the imaginary part is null: 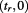 which indicates infinite and inert space that is the ground state of matter particles that are then described by
which indicates infinite and inert space that is the ground state of matter particles that are then described by 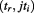 , or:
, or: 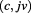 , or also:
, or also: 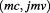 , which means that they are internally being re-created at the speed of light, that is the real part, and moving outwardly at the imaginary apparent velocity
, which means that they are internally being re-created at the speed of light, that is the real part, and moving outwardly at the imaginary apparent velocity
 that is given by equation 5.3. Vacuum is therefore when this apparent velocity, or momentum, becomes absolutely zero, both as the object’s total velocity and any vector velocities of its constituents, and this corresponds to zero absolute temperature.
that is given by equation 5.3. Vacuum is therefore when this apparent velocity, or momentum, becomes absolutely zero, both as the object’s total velocity and any vector velocities of its constituents, and this corresponds to zero absolute temperature.
The representation of space-time, involving imaginary time, as Euclidean space having 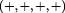 signature:
signature: 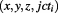 , was used in the early formulation of Special Relativity by Poincaré and even Minkowski, but because there were no substantial reasons to treat time as imaginary, Minkowski had to introduce the four-dimensional space-time:
, was used in the early formulation of Special Relativity by Poincaré and even Minkowski, but because there were no substantial reasons to treat time as imaginary, Minkowski had to introduce the four-dimensional space-time: 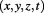 , with Lorentzian metric with signature
, with Lorentzian metric with signature 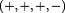 , in which time and space are treated equally. This four dimensional space later becomes necessary for General Relativity, due to the presence of gravity which required Riemannian geometry.
, in which time and space are treated equally. This four dimensional space later becomes necessary for General Relativity, due to the presence of gravity which required Riemannian geometry.
The non-Euclidean Minkowski space is therefore the first global approximation of the metaphysical reality, just as the Euclidean Minkowski space is a local approximation when the effect of gravity is neglected, while the Galilean space is the classical approximation for non-relativistic velocities. These three relative approximations are still serving very well in describing the respective physical phenomena, but they can not describe the actually metaphysical reality of the Universe. As Hawking noticed: “In fact one could take the attitude that quantum theory and indeed the whole of physics is really defined in the Euclidean region and that it is simply a consequence of our perception that we interpret it in the Lorentzian regime.” Hawking (1979).
Hyperbolic geometry was developed in the process of trying to prove the parallel postulate of Euclid. Some geometers tried to prove it by assuming its negation and trying to derive a contradiction. All attempts in this regard failed, including those made by Proclus, Ibn al-Haytham, Omar Khayyám, Nasir al-Din al-Tusi, Witelo, Gersonides, Alfonso, Giovanni Saccheri, John Wallis, Johann Lambert, and Legendre. The parallel postulate is not provable from the other postulates, but these efforts led to the discovery of hyperbolic geometry, but the term “hyperbolic geometry” was introduced by Felix Klein in 1871, where he use the transformations of projective geometry to produce isometries. The idea used a conic section or quadric to define a region, and used cross ratio to define a metric.
The discovery of hyperbolic geometry had important philosophical consequences. Many philosophers viewed philosophical rigor in terms of the geometrical method of reasoning used in Euclid’s Elements. However, because Euclidean, hyperbolic and elliptic geometry are all consistent, the question arises: which is the real geometry of space, and if it is hyperbolic or elliptic, what is its curvature? In his sphere-world thought experiment, Poincaré came to the conclusion that everyday experience does not necessarily rule out other geometries. The geometrization conjecture gives a complete list of eight possibilities for the fundamental geometry of our space.
List of Some Major Problems Solved by the Duality of Time Theory
In the following articles, we will list some of the major unsolved problems in theoretical physics and describe them in brief, stating their potential solutions according to the Duality of Time Postulate. Although many of these problems will be simply eliminated according to the new genuinely-complex time-time geometry, a detailed theoretical and mathematical analysis is required in order to explain how these problems are settled. Therefore, some of the following brief suggested solutions may be speculative.
These articles are extracted from Chapter III of the Duality of Time
book, and some of the details are discussed further in other chapters, as well as Volume III that is the Ultimate Symmetry. A more concise description is also published in Time Chest.
The Duality of Time Postulate

To understand how all these major problems could be solved so easily, please study first the Duality of Time Postulate, that has been extracted from Chapter V of the Duality of Time
book.

Other Pages Related to Search Keywords:
... e To understand how all these major problems could be solved so easily, please study first the Duality of Time Postulate , that has been extracted from Chapter V of the Duality of Time book. ...
... postulates, but these efforts led to the discovery of hyperbolic geometry, but the term “hyperbolic geometry” was introduced by Felix Klein in 1871, where he use the transformations of PROJECTIVE GEOMETRY to produce isometries. The idea used a conic section or quadric to define a regi ...
... ce is therefore the first global approximation of the metaphysical reality, just as the Euclidean Minkowski space is a local approximation when the effect of gravity is neglected, while the Galilean space is the classical approximation for non-relativistic velocities. These three relative ...
... tent with relation to the real flow of time that is creating space and matter. Therefore, the non-Euclidean Minkowski space-time coordinates will be a special approximation of the Euclidean SPACE COORDINATES , or time coordinates: where or represent the inner real part of time: , and repre ...
... Euclid. Some geometers tried to prove it by assuming its negation and trying to derive a contradiction. All attempts in this regard failed, including those made by Proclus, Ibn al-Haytham, Omar Khayyám, Nasir al-Din al-Tusi, Witelo, Gersonides, Alfonso, Giovanni Saccheri, John Wallis, Jo ...
... ginary time, as Euclidean space having signature: , was used in the early formulation of Special Relativity by Poincaré and even Minkowski, but because there were no substantial reasons to TREAT TIME as imaginary, Minkowski had to introduce the four-dimensional space-time: , with Lorentzi ...
... ace-time, involving imaginary time, as Euclidean space having signature: , was used in the early formulation of Special Relativity by Poincaré and even Minkowski, but because there were no SUBSTANTIAL REASONS to treat time as imaginary, Minkowski had to introduce the four-dimensional spac ...
... es absolutely zero, both as the object’s total velocity and any vector velocities of its constituents, and this corresponds to zero absolute temperature. The representation of space-time, INVOLVING IMAGINARY time, as Euclidean space having signature: , was used in the early formulation o ...
... stated, imaginary and complex refer to these hyperbolic numbers . Hyperbolic geometry was used in the early formulation of Special Relativity to represent Lorentz boost as a rotation in the IMAGINARY PLANE , but it will be shown in section 2 below that under the new Euclidean complex-time f ...
... metaphysical reality, just as the Euclidean Minkowski space is a local approximation when the effect of gravity is neglected, while the Galilean space is the classical approximation for non- RELATIVISTIC VELOCITIES . These three relative approximations are still serving very well in describi ...
... dimensional space later becomes necessary for General Relativity, due to the presence of gravity which required Riemannian geometry. The non-Euclidean Minkowski space is therefore the first GLOBAL APPROXIMATION of the metaphysical reality, just as the Euclidean Minkowski space is a local a ...
... tion in the imaginary plane, but it will be shown in section 2 below that under the new Euclidean complex-time frame, Lorentz transformations will be valid between inertial and non-inertial FRAMES ALIKE , because the dynamic relation between the real and imaginary parts of time implies that ...











