Solving the Arrow of Time Problem Based on the Duality of Time Theory
The following article is extracted from Chapter III of the Duality of Time book, and some of the details are discussed further in other chapters, as well as Volume III that is the Ultimate Symmetry.
 The second law of thermodynamics states that, in isolated systems, the total entropy can only increase over time.
Entropy is related to the number of microscopic configurations that a thermodynamic system can have when in a state as specified by some macroscopic variables.
In the modern microscopic interpretation of entropy in statistical mechanics, entropy is the amount of additional information needed to specify the exact physical state of a system, given its thermodynamic specification.
The second law of thermodynamics states that, in isolated systems, the total entropy can only increase over time.
Entropy is related to the number of microscopic configurations that a thermodynamic system can have when in a state as specified by some macroscopic variables.
In the modern microscopic interpretation of entropy in statistical mechanics, entropy is the amount of additional information needed to specify the exact physical state of a system, given its thermodynamic specification.
The second law of thermodynamics is one of the fundamental laws of nature. After developing General Relativity, in the 1920s, many theoretical physicists, including Einstein, considered the possibility of cyclic models in which the universe follows indefinite self-sustaining cycles of eternal series of expansion and contraction. These models were soon excluded because they clearly contradict this fundamental law.
One important puzzle associated with the second law of thermodynamics is the entropic arrow of time, because it requires a particular direction for time, unlike most other laws of physics which are time-symmetric. The Arrow of Time concept was developed by Arthur Eddington (1882-1944 AD) in 1927 and it is still an unsolved general physics problem.
The Duality of Time is intrinsically built on one time direction, both for the inner and outer levels, and the arrow of time is explicitly expressed in the equations that will also show how two orthogonal arrows of time combine to make one (two-directional) dimension of space. We have also discussed the entropic and other similar arrows of time that result from various other natural phenomena when we reviewed modern physics and cosmology in chapter III (of the Duality of Time book).
Although most physics laws are time-symmetrical, time itself is evidently one directional. There are many experimental observations with one arrow of time, such as the second law of Thermodynamics, or the fact that entropy always increases. The entropy of the Universe was very low in the past, and time correlates with the universal increase in entropy, from the past and to the future.
Moreover, in certain weak force decays, there are some interactions with clear Charge-Parity violations. Why this is not observed in other interactions. These CP violations do not seem to be related with the Second Law of Thermodynamics.
Furthermore, the collapse of wave-function is also irreversible, and this quantum arrow of time also seems to be independent from the thermodynamic arrow.
So are these arrows of time separate or how they are related? Are there exceptions to the principle of causality? Is there a single possible past? Is the present moment physically distinct from the past and future, or is it merely an emergent property of consciousness?
The Duality of Time Solution
The concept of time is the most fundamental problem in physics and cosmology, and the current theories do not provide any detailed explanation of the the nature of time. For this reason, the Duality of Time Theory is the first to explain the real flow of time. In this theory, time is naturally one-directional, both in the normal level and on the inner dimensions where space and matter are perpetually being re-created in one linear chronological order.
The arrow of time will be expressed explicitly in the mathematical formulations in chapter V (of the Duality of Time book), although a reverse arrow of time will be also defined, and it will be shown how each two opposite time directions dynamically create one dimension of space, so in total we can conceive of seven levels of time: six inner levels for the three spatial dimensions, and one outer level for the normal time direction.
Moreover, because all the fundamental interactions are explained in terms of space-time geometry, and not only gravity, parity does not have any meaning for the weak interaction because it is one dimensional space, and the line does not have left or right sides, unlike the plane and volume where the other interactions are exhibited. This relation of the fundamental interactions with dimensionality can also solve the problem of hierarchy as we have seen in this article.
Discreteness implies interruption or discontinuity, and this is what the outer time is doing to the continuous flow of the inner time that is perpetually re-creating space and matter in one chronological sequence. Mathematically, this is achieved by multiplying with the imaginary unit, which produces an abrupt rotation by 90 degrees, creating a new dimension that is orthogonal on the previous level. Multiplying with the imaginary unit again causes time to become real again, i.e. like space. This means that each point of our 3D+1 space-time is the combination of seven dimensions of time, the first six are the real levels which make the three spatial dimensions t_r=sqrt{(x/c)^2+(y/c)^2+(z/c)^2}, and the seventh is the imaginary level that is the outer time t_i.
This outward (normal) level of time, t_i, is interrupting and delaying the real flow of time, t_r, so it can not exceed it, because they both belong to one single existence that is flowing either in the inward levels to form the continuous (real) spatial dimensions, or in the outward level to form the imaginary discrete time, not the two together; otherwise they both would be real as we are normally deceived. As we introduced in the postulate, the reason for this deception is because we only observe the physical dimensions, in the outer time, after they are created in the inner time, so we "imagine" them to be co-existing continuously, when in fact they are being sequentially re-created. It is not possible otherwise to obtain self-contained and granular space-time, whose geometry could be defined without any previous background topology. Thus, we can write:
0< t_i < t_r.
So because t_i is interrupting and delaying t_r, the actual (net value of) time is always smaller than the real time: |t_c|=sqrt{t_r^2-t_i^2} < t_r, and this is actually the proper time as defined in Special Relativity.
The Two Orthogonal Arrows of Time
However, it should be noted here that, unlike the case for normal complex (Euclidean) plane, the modulus of split-complex numbers is different from the norm, because it is not positive-definite, but it has a metric signature (1, -1). This means that, although our normal time is flowing only in one direction because it is interrupting the real flow of creation and can not exceed it, it is still possible to have the orthogonal state where the imaginary time is flowing at the speed of creation and the real part is interrupting it, such that: t_c=t_i+jt_r, so: |t_c|=sqrt{t_i^2-t_r^2}, and then t_r < t_i, from our perspective.
In this case, the ground state of that vacuum would be (0, c), which describes anti-matter as we shall explain further in this article, where we speak about super-symmetry and its breaking.
 Equivalently, as another equivalent reason for the arrow of time, the apparent velocity v can not exceed c because it is the average of all instantaneous velocities of all individual geometrical points that constitute the object, which are always fluctuating between 0 and c; so by definition v is capped by c, as explained with detailed mathematical formulation in Chapter V of the Duality of Time book as well as Chapter II of the Ultimate Symmetry.
Equivalently, as another equivalent reason for the arrow of time, the apparent velocity v can not exceed c because it is the average of all instantaneous velocities of all individual geometrical points that constitute the object, which are always fluctuating between 0 and c; so by definition v is capped by c, as explained with detailed mathematical formulation in Chapter V of the Duality of Time book as well as Chapter II of the Ultimate Symmetry.
So the imaginary time, t_i, is acting like a resistance against the perpetual re-creation of space, and its interruption, i.e. going in the outward level of time, is what causes physical motion and the inertial mass m_0, which then effectively increases with the imaginary velocity, and when the outward imaginary time approaches the inner time, the apparent velocity v approaches the speed of creation c, and m approches infinity.
If this extreme state could ever happen (but not by acceleration, as we shall see further below), the system would be described by (c, c), which means that both the real and imaginary parts of the complex-time would be continuous, and this describes another homogeneous Euclidean space with one higher dimension than the original (c, 0) vacuum.
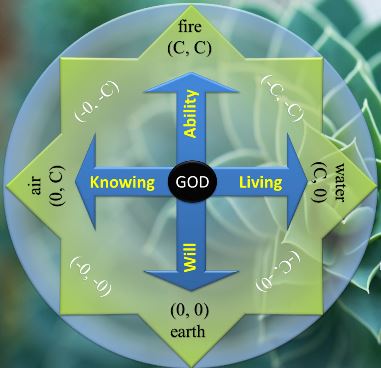
Actually, the hyperbolic split-complex number (c, c) denotes a non-invertible null vector that describes the asymptotes, whose modulus equals zero, since both its real and imaginary parts are equal. At the same time, as a normal complex number, (c, c) describes an isotropic infinite and inert Euclidean space (without time), because its dimensions are continuous, or uninterrupted. The metaphysical entities of the Universe are sequentially oscillating between the two vacuum states (as Euclidean spaces or normal complex numbers): (c, 0) and (c, c), while collectively they appear to be evolving according to the physical (hyperbolic) space-time states (c, v), as split-complex numbers.
Therefore, the vacuum state can be described either as the non-invertible vector (c, c) in the hyperbolic plane H, and that is equal to one absolute point from the time perspective (when we look at the World from outside), or an isotropic Euclidean space (c, 0) as normal complex numbers set C, but with one lower dimension, and that is the space perspective (when we look from inside).
Infinities and singularities occur when we confuse between these two extreme views; because if the observer is situated inside a spatial dimension it will appear to them continuous and infinite, while it forms only one discrete state in the encompassing outer time.
As we have demonstrated in Chapter III of the Ultimate Symmetry, General Relativity is the first approximation for inside observers, but since the Universe is evolving we need to describe it by H, from the time perspective. So General Relativity is correct at every single instance of time (only), because the resulting instantaneous space is continuous, but when the outward time flows these instances will form a series of discrete states that should be described by Quantum Field Theory. If we combine these two descriptions properly, we should be able to eliminate singularities and infinities from General Relativity and Quantum Field Theory.
In other words, the whole homogeneous space forms a single point in the outer time, and our physical Universe is the dynamic combination of these two extreme states, denoted as space-time. This is the same postulated statement that the geometrical points are perpetually and sequentially fluctuating between 0 (for time) and c (for space), and no two points can be in the state of (existence in) space at the same real instance of time, so the points of space come into existence in one chronological sequence, and they can not last in this state for more than one single moment of time, thus they are being perpetually re-created.
Nonetheless, since it is not possible to accelerate a physical object (to make all its geometrical points) to move at the speed of creation c, one alternative way to reach this speed of light, and thus make a new spatial dimension, is to combine the two orthogonal states (c, 0) and (0, c), which is the same as matter-antimatter annihilation, and this is a reversible interaction that can be described by the following equation:
(c, 0)+(0, c) = (c, c)+(0, 0).
Super-symmetry and the Three Conclusive Time-Time Combinations
In conclusion, we can distinguish three conclusive scenarios for the complex flow of time:
1- In our usual space-time where matter particles are described by (c, v), we are restricted by the normal arrow of time because t_i<t_r.
2- In the orthogonal arrow of time, when t_i>t_r, from our perspective, the vacuum state is described by (0, c), which can be excited to (v, c) that describes the states of anti-matter.
3- When t_i=t_r, we get the Euclidean space (c, c), which is equivalent to the initial vacuum state (c, 0), but with one higher spatial dimension. This, however, can not happen by means of mechanical motion, but by combining the two orthogonal times
Therefore, there are two orthogonal arrows of time (c, 0) and (0, c), that can combine and split between the states of (0, 0) and (c, c), which all together correspond to the four elemental states, or classical elements, whose quintessence is the Single Monad.
In the following articles, we will list some of the major unsolved problems in theoretical physics and describe them in brief, stating their potential solutions according to the Duality of Time Postulate. Although many of these problems will be simply eliminated according to the new genuinely-complex time-time geometry, a detailed theoretical and mathematical analysis is required in order to explain how these problems are settled. Therefore, some of the following brief suggested solutions may be speculative.
To understand how all these major problems could be solved so easily, please study first the Duality of Time Postulate, that has been extracted from Chapter V of the Duality of Time
book.
... e To understand how all these major problems could be solved so easily, please study first the Duality of Time Postulate , that has been extracted from Chapter V of the Duality of Time book. ...
... m of Physical Information The Problem of Causality The Planck Scale Problem Problem of Magnetic Monopoles EPR and the Problem of Non-Locality Problem of Quantum Gravity Mass Generation Mechanism Homogeneity and the Horizon Problem Problem of Neutrino Mass ...
... the past, and time correlates with the universal increase in entropy, from the past and to the future. Moreover, in certain weak force decays, there are some interactions with clear Charge-Parity violations. Why this is not observed in other interactions. These CP violations do not seem t ...
... cribes the asymptotes, whose modulus equals zero, since both its real and imaginary parts are equal. At the same time, as a normal complex number, (c, c) describes an isotropic infinite and inert Euclidean space (without time), because its dimensions are continuous, or uninterrupted. The m ...
... le null vector that describes the asymptotes, whose modulus equals zero, since both its real and imaginary parts are equal. At the same time, as a normal complex number, (c, c) describes an ISOTROPIC INFINITE and inert Euclidean space (without time), because its dimensions are continuous, ...
... ace with one higher dimension than the original (c, 0) vacuum. Actually, the hyperbolic split-complex number (c, c) denotes a non-invertible null vector that describes the asymptotes, whose MODULUS EQUALS zero, since both its real and imaginary parts are equal. At the same time, as a norma ...
... d this describes another homogeneous Euclidean space with one higher dimension than the original (c, 0) vacuum. Actually, the hyperbolic split-complex number (c, c) denotes a non-invertible NULL VECTOR that describes the asymptotes, whose modulus equals zero, since both its real and imagin ...
... tinuous, and this describes another homogeneous Euclidean space with one higher dimension than the original (c, 0) vacuum. Actually, the hyperbolic split-complex number (c, c) denotes a non- INVERTIBLE NULL vector that describes the asymptotes, whose modulus equals zero, since both its real ...
... sly, when in fact they are being sequentially re-created. It is not possible otherwise to obtain self-contained and granular space-time, whose geometry could be defined without any previous BACKGROUND TOPOLOGY . Thus, we can write: 0< t_i < t_r. So because t_i is interrupting and dela ...
... continuously, when in fact they are being sequentially re-created. It is not possible otherwise to obtain self-contained and granular space-time, whose geometry could be defined without any PREVIOUS BACKGROUND topology. Thus, we can write: 0< t_i < t_r. So because t_i is interrupting ...
... the postulate , the reason for this deception is because we only observe the physical dimensions, in the outer time, after they are created in the inner time, so we "imagine" them to be co- EXISTING CONTINUOUSLY , when in fact they are being sequentially re-created. It is not possible other ...
... between the two vacuum states (as Euclidean spaces or normal complex numbers): (c, 0) and (c, c), while collectively they appear to be evolving according to the physical (hyperbolic) space- TIME STATE s (c, v), as split-complex numbers. Therefore, the vacuum state can be described either as ...



 The second law of thermodynamics states that, in isolated systems, the total entropy can only increase over time.
Entropy is related to the number of microscopic configurations that a thermodynamic system can have when in a state as specified by some macroscopic variables.
In the modern microscopic interpretation of entropy in statistical mechanics, entropy is the amount of additional information needed to specify the exact physical state of a system, given its thermodynamic specification.
The second law of thermodynamics states that, in isolated systems, the total entropy can only increase over time.
Entropy is related to the number of microscopic configurations that a thermodynamic system can have when in a state as specified by some macroscopic variables.
In the modern microscopic interpretation of entropy in statistical mechanics, entropy is the amount of additional information needed to specify the exact physical state of a system, given its thermodynamic specification. 







